» Магические квадраты
|
В этом разделе мы приводим результаты из некоторых новых статей о магических квадратах, которые удалось найти. Эти статьи показывают, что магические квадраты и их обобщения изучаются и в настоящее время. В статье [8] приведен список нерешенных проблем о магических квадратах.
В статье [6] изучается операция конкатенации магических квадратов. Под операцией конкатенации (программистский термин) двух строк или столбцов некоторого магического квадрата автор понимает операцию приписывания к элементам первой строки (столбца) элементов второй строки (столбца). Пусть, например, 
Это столбцы магического 
квадрата. Тогда 
, 
и так далее. Оказывается, 
.
Это же свойство постоянства суммы элементов сохраняется для всех пар конкатенированных столбцов и строк вышеприведенного магического квадрата, т.е. 
для любых 
.
Приведен пример магического мультимпликативного 
квадрата (т.е. магического квадрата относительно умножения элементов его строк, столбцов и диагоналей) с аналогичными свойствами.
В статье [7] изучаются антимагические квадраты. Антимагическим квадратом называется таблица размера 
, элементами которой являются натуральные числа от 
до 
расположенные таким образом, что суммы всех чисел в каждой строке, каждом столбце и по двум главным диагоналям образуют множество последовательных натуральных чисел.
Например, числа 
образуют антимагический 
квадрат с множеством сумм 
.
Автор нашел метод построения антимагического квадрата любого порядка, указал метод построения антимагических квадратов любого четного порядка большего 4. Доказал, что для каждого четного 
этим методом можно построить 2 вида антимагических квадратов.
В статье [9] построен чисто пандиагональный квадрат:
8 |
6 |
2 |
4 |
7 |
5 |
1 |
3 |
15 |
13 |
9 |
11 |
16 |
14 |
10 |
12 |
По всем восьми диагоналям этого квадрата суммы чисел равны 34, а суммы чисел стоящих в столбцах и строках этого квадрата числу 34 не равны.
Янош Больяи открыл следующий магический квадрат.
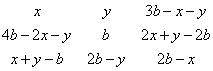
В стватье [10] каждому магическому квадрату 
сопоставляется квадратная матрица 
состоящая из тех же элементов, что и магический квадрат 
. Изучаются матрицы размера 
. В статье доказано, что если 
есть матрица магического квадрата, то 
также есть матрица магического квадрата тогда и только тогда, когда 
- нечетное число.
В заметке [11] построен магический квадрат с магической суммой равной 2001.
12 |
990 |
15 |
984 |
11 |
988 |
O1 |
1001 |
982 |
20 |
992 |
7 |
996 |
3 |
993 |
9 |
